ABC050 D XorSum に歯がたたずとりあえず桁DPに慣れることにした。
桁DP
Nまでの整数の中にこういう条件を満たす数字は何個あるか、みたいなのが桁DPの出番らしい。順番に各桁の数字をみて場合分けしていくというのが基本的なアイデアのようだ。
ABC007 D 禁止された文字
- A..B間に4と9を含む数字はいくつあるか
どんなパターンがあるのか
ここでAB間というのを無視してある数字N以下とし、桁DPのことはとりあえず脇に置いて場合分けを試みると以下の図の左のようになる。
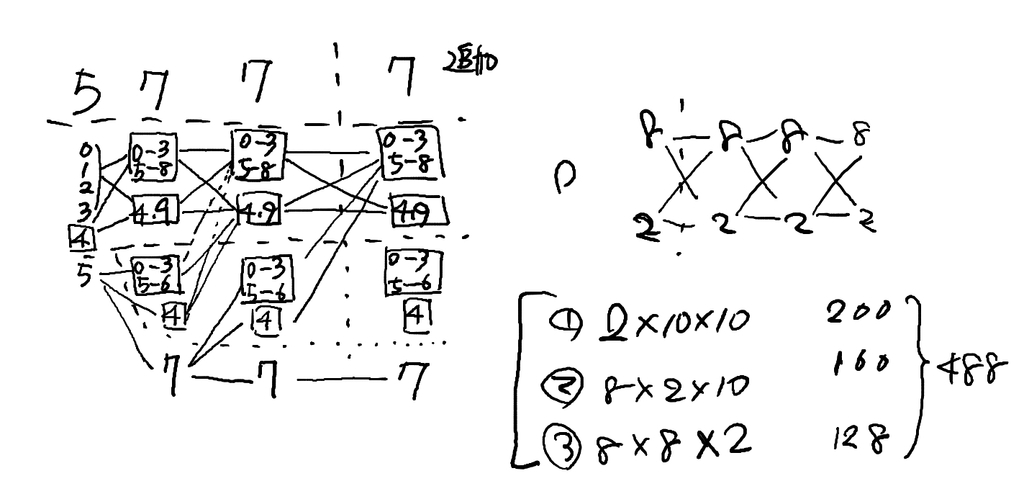
とりあえず577として頭から見ていくと5より前の01234 については4xxは全部が4を含む。0xx 1xx 2xx 3xxはxxの部分については同じパターンを持ってる。各桁4と9が2個,それ以外が8個なので、あるのは2 * 10+8 * 2。これは桁が増えていくと図の右のようなパターンで増えていく。たとえば1000の場合 、先頭の0 の下に来るパターンは 2 * 10 * 10 + 8 * 2 * 10 + 8 * 8 * 2 となって、合計488。出力例3の数字と一致する。
図ではパターンが交差しているが、これは同じパターンだから再利用しているだけで、たとえば577で最初に0xx、1xx、 .. 4xx のことを考えて場合の数を出してしまえば後は放置していい。桁が増えればこのパターンが図の右上のようにのびていくだけで、そこにもパターンがあって、2 * ( ∑( i=0→k )(8i * 10k-i ) ) みたいな感じになるので適当に計算できる。
次考えるのは577 の二桁目の7つまり500台の70未満についてだが、同様に 0-3,5,6と4に分けれ、前者については それぞれ2通り 、4については 10通りある。同様に最後577の三桁目の7未満、つまり 570台の7未満について考えると同じようになる。最後に577について場合分けする。桁を下っていくと枝分かれした分のパターンがどんどん短かくなっていくだけなので、最初にパターンがわかればあとは応用していくだけで、別にDPっぽいことをせずとも計算するだけはできる。
桁DPでのパターン分け
というわけで桁DPですが、その前に桁DPはここで勉強しました。やってることは同じです。pekempeyサンプルを写経のためにpythonでゴリゴリ書きなおしたのは附録で最後につけています。
実は桁DPも上の場合分けとやってることは同じになる。この場合dp[i][j][k]と三つ箱を用意する。先頭の[i]が桁。真ん中の[j]がN未満かそうでないか。最後の[k]が4,9を含むか含まないか。これに各桁の0-9の数字をグルグルまわして場合の数を前の桁の倍倍にしていく。上の図左でいうと大きく桁を書いている縦の列が[i]。場合分けのごちゃごちゃしたところの下にある5 7 7 と大きく書いてあるラインがN未満?のときの場合分けで、5-7-7のラインの上に来ているのがN未満に分類された場合分けになる。上限をNで切っているのでN未満でない数は常に1になるのだが、なんでこんな場合分けになるかというと577の先頭で0-4と5に分けたとき、0-4の下にある数字はそれぞれ100で、求めたい場合分けの数もすぐ計算できるが、5の下にあるのはさらに細かく分けていかないとわからないからだ。
さらにその次の[k]にあたる4,9かそうでないかは、上図左のごちゃごちゃしたところの 4の四角もしくは4,9の四角がそれに相当する。これで各桁の0-9について、その前の桁の場合分けの数を分配していくから、たとえば既に4か9が出現している場合の場合の数は k=1 の箱の総取りになり、前の桁の場合の数の10倍になる。出ていないときはk=0の箱が8倍、k=1の箱が2倍になる。
dp[0][0][0] = 1
for i in range(iL):
for j in range(2):
iLim = 9 if j else int(sU[i])
for k in range(2):
for d in range(iLim + 1):
dp[i+1][j or d < iLim][k or d in {4,9}] += dp[i][j][k]
桁DP の亜流
深い for 文を展開して底を浅くする流派もあるようだ。上に書いたループを添字j,kを使わずこんな風に展開する。
dp[0][0][0] = 1
for i in range(iL):
for d in range(10):
dp[i+1][1][1] += dp[i][1][1]
if d in {4,9}:
dp[i+1][1][1] += dp[i][1][0]
else:
dp[i+1][1][0] += dp[i][1][0]
iLim = int(sU[i])
for d in range(iLim + 1):
dp[i+1][d<iLim][1] += dp[i][0][1]
if d in {4,9}:
dp[i+1][d<iLim][1] += dp[i][0][0]
else:
dp[i+1][d<iLim][0] += dp[i][0][0]
いいところは例えばこんな風に自明なところのループを省略して計算量を減らせる点だ。悪い点は見た目が怖い。
dp[0][0][0] = 1
for i in range(iL):
dp[i+1][1][1] += dp[i][1][1] * 10
dp[i+1][1][1] += dp[i][1][0] * 2
dp[i+1][1][0] += dp[i][1][0] * 8
iLim = int(sU[i])
dp[i+1][1][1] += dp[i][0][1] * iLim
dp[i+1][0][1] += dp[i][0][1]
for d in range(iLim + 1):
if d in {4,9}:
dp[i+1][d<iLim][1] += dp[i][0][0]
else:
dp[i+1][d<iLim][0] += dp[i][0][0]
桁dpの中でこういう風に展開する流派をどうよぶのかわからないが見た目が怖くてしかも速くなるので好きな人は好きなんじゃなかろうか。
他にも再帰の流派がありそっちの方が複雑な操作はしやすいらしい。まだよくわからん。しかしこういうのどこまでdpと呼んでいいのやら。たとえばこのページで最初書いたパターン分けで直接計算していくのはdpでも再帰でもないわけですが、基本的な考え方は同じになる。まぁたぶん再利用してるかどうかというのは大きな分かれ目で、メモ化再帰がdpと同一視されるのも再利用の点だけに注目するからだろう。ということで自分が最初に書いた考え方で再利用してるのは説明図の中と、関数化してしまったところだけなので、こういうのまではdpと言わないのかもしれない。

数学ガールの秘密ノート/場合の数 (数学ガールの秘密ノートシリーズ)
- 作者: 結城浩
- 出版社/メーカー: SBクリエイティブ
- 発売日: 2016/04/20
- メディア: 単行本
- この商品を含むブログ (8件) を見る

- 作者: 結城浩
- 出版社/メーカー: SBクリエイティブ
- 発売日: 2013/12/18
- メディア: 単行本
- この商品を含むブログ (17件) を見る
附録 pekempey サンプルをpython3でそのまま書いた
iA = 4275631 sA = str(iA) iL = len(sA) #1 A以下の非負整数 dp1 = [[0] * 2 for _ in range(iL+1)] # i 上からi桁目まで見ている # j A未満であることが確定している # 0 してない # 1 している dp1[0][0] = 1 #種 for i in range(iL) : for j in range(2) : # j= 0 1 # j 0のとき A[i桁目] # j 1のとき9 iLim = 9 if j else int(sA[i]) # 0 0-A[i桁目]まで舐める # 1 0-9まで全部舐める for d in range(iLim+1) : dp1[i + 1][j or d < iLim] += dp1[i][j] # j 0 -> d < iLim #A[i桁目]未満で1 A[i桁目]のとき0 # j 1 -> 10倍 iAns = 0 for j in range(2) : iAns += dp1[iL][j] #for a in dp1 : # print (" ".join([str(_) for _ in a])) print("#1 ",iAns) # dp1 # 1 0 #4 1 4 #2 1 42 #7 1 427 #5 1 4275 #6 1 42756 #3 1 427563 #1 1 4275631 #2 A以下の非負整数のうち 3の付く数の総数 dp2 = [[[0]*2 for _ in range(2) ] for _ in range(iL +1)] # i 上からi桁目まで見ている # j A未満であることが確定している # k すでに3を選んでいる dp2[0][0][0] = 1 for i in range(iL): for j in range(2): for k in range(2): # j 0のとき A[i桁目] # j 1のとき9 iLim = 9 if j else int(sA[i]) # 0 0-A[i桁目]まで舐める # 1 0-9まで全部舐める for d in range(iLim + 1): dp2[i+1][j or d < iLim][k or d == 3] += dp2[i][j][k] # j 0 -> d < iLim # A[i桁目]未満で1 # A[i桁目]のとき0 # k 0 #既に3を選んでいないとき d==3のとき 1 # k 1 #既に選んでいるとき全部 # j 1 -> 0-9に対してkの操作 iAns = 0 for j in range(2) : iAns += dp2[iL][j][1] #for a in dp2 : # print(a) print("#2 ",iAns) # dp2 # [[1, 0], [0, 0]] #4 [[1, 0], [3, 1]] #2 [[1, 0], [29, 13]] #7 [[1, 0], [267, 160]] #5 [[1, 0], [2407, 1868]] #6 [[1, 0], [21668, 21088]] #3 [[0, 1], [195015, 232548]] #1 [[0, 1], [1755135, 2520496]] # 3 A以下の非負整数のうち、3がつくまたは3の倍数 dp3 = [[[[0]*3 for _ in range(2)] for _ in range(2) ] for _ in range(iL +1)] # i 上からi桁目まで見ている # j A未満であることが確定している # k すでに3を選んでいる # l mod3の値(0..2) dp3[0][0][0][0] = 1 for i in range(iL): for j in range(2): for k in range(2): for l in range(3): # j 0のとき A[i桁目] # j 1のとき9 iLim = 9 if j else int(sA[i]) # 0 0-A[i桁目]まで舐める # 1 0-9まで全部舐める for d in range(iLim + 1): #dp3[i+1][j or d < iLim][k or d==3][(l*10+d) % 3] += dp3[i][j][k][l] dp3[i+1][j or d < iLim][k or d==3][(l+d) % 3] += dp3[i][j][k][l] # j 0 -> d < iLim # A[i桁目]未満で1 # A[i桁目]のとき0 # k 0 #既に3を選んでいないとき d==3のとき 1 # k 1 #既に選んでいるとき全部 # l 0 l+d は3の場合 l*10+dと同じ 上の桁の余りに下の桁を足してそこから次の剰余を出す # l 1 # l 2 # j 1 -> 0-9に対してk,lの操作 iAns = 0 for j in range(2) : for k in range(2): for l in range(3): if k or l ==0 : #k 1 既に3を選んでいるとき全部 #k 0 既に3を選んでいないときはlが0(3の倍数)のとき iAns += dp3[iL][j][k][l] #for a in dp3 : # print(a) print("#3 ",iAns) # 4 A以下の非負整数のうち、[3がつくまたは3の倍数] かつ [8の倍数でない] dp4 = [[[[[0]*8 for _ in range(3)] for _ in range(2)] for _ in range(2) ] for _ in range(iL +1)] # i 上からi桁目まで見ている # j A未満であることが確定している # k すでに3を選んでいる # l mod3の値(0..2) # m mod3の値(0..7) dp4[0][0][0][0][0] = 1 for i in range(iL): for j in range(2): for k in range(2): for l in range(3): for m in range(8): # j 0のとき A[i桁目] # j 1のとき9 iLim = 9 if j else int(sA[i]) # 0 0-A[i桁目]まで舐める # 1 0-9まで全部舐める for d in range(iLim + 1): dp4[i+1][j or d < iLim][k or d==3][(l+d) % 3][(m*10 +d) % 8] += dp4[i][j][k][l][m] iAns = 0 for j in range(2) : for k in range(2): for l in range(3): for m in range(8): if( k or l ==0 ) and ( m != 0 ) : iAns += dp4[iL][j][k][l][m] #for a in dp4 : # print(a) print("#4 ",iAns)